Contoh Soal UTBK SNBT Penalaran Matematika 2024

Salah satu subtes yang muncul pada UTBK SNBT 2024 adalah Penalaran Matematika. Simak latihan soal dan pembahasan lengkapnya di artikel ini.

—

Halo, teman-teman! Sudah tahu apa aja sub tes yang akan diujikan pada UTBK SNBT mendatang? Terdapat 4 materi tes skolastik yang diujikan, salah satunya Penalaran Matematika. Hmm, kira-kira seperti apa ya contoh soal dan cara mengerjakannya?

 

Apa itu Penalaran Matematika?

Penalaran Matematika adalah soal yang menguji kemampuan calon mahasiswa dalam menerapkan matematika dasar untuk memecahkan masalah di kehidupan sehari-hari. Jenis soal ini sudah kamu pelajari di bangku SMP dan SMA, jadi tak serumit soal SNBT tahun sebelumnya.

Penalaran Matematika mengharuskan kamu untuk menggunakan logika dan kemampuan berhitung. Tips mengerjakan soal ini yaitu:

1. Garisbawahi kata kunci yang terdapat pada soal.
2. Uraikan rumus dan pernyataan dalam bentuk coretan agar bisa menjawab soal dengan mudah.
3. Bila perlu, hitung semua pilihan jawaban yang ada supaya lebih yakin.
4. Meskipun terlihat mudah, kerjakan soal dengan teliti.

 

Latihan Soal Penalaran Matematika

Ingat ya, untuk bisa menjawab penalaran matematika dengan benar, kamu harus berlatih dengan variasi soal yang berbeda. Nah, apa saja sih kisi-kisi atau materi yang kemungkinan keluar di sub-tes ini? Yuk, simak pembahasannya!

Baca juga: Tips Mengerjakan Soal Penalaran Matematika, Pasti Bisa!

1. Contoh Soal Isian Penalaran Matematika (NEW!)

Subtopik : Aljabar

Level Kognitif : HOTS

Perhatikan teks berikut!

Yoga memiliki wadah-wadah dengan tiga ukuran yang berbeda, yaitu S, M, dan L. Diketahui massa wadah berukuran M adalah dua kali lipat massa wadah berukuran S dan setiap wadah dengan ukuran yang sama memiliki massa yang sama.

Ia kemudian menimbang kombinasi dua wadah dari wadah-wadah yang dimilikinya pada timbangan digital dan didapat hasil sebagai berikut.

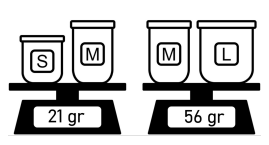
Jika Yoga menimbang 2 wadah berukuran L bersama-sama, massa kedua wadah tersebut adalah … gram.

Catatan: Hanya diisi dengan angka (contoh: 10)

 

Kunci Jawaban : 84

Pembahasan :

Misalkan x, y, dan z secara berurutan menyatakan massa wadah S, M, dan L. Berdasarkan gambar pada soal, didapat persamaan-persamaan sebagai berikut.

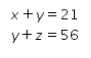
Kemudian, diketahui massa wadah berukuran M adalah dua kali lipat massa wadah berukuran S maka diperoleh . Akibatnya nilai dari dapat ditentukan dengan substitusi ke persamaan sebagai berikut.

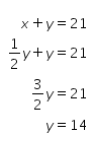
Selanjutnya, substitusi y = 14 ke persamaan y + z = 56 sebagai berikut.

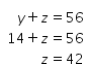
Diperoleh z = 42, dengan kata lain massa dari wadah berukuran L adalah 42 gram. Oleh karena itu, jika dua wadah berukuran L ditimbang bersama-sama, massa kedua wadah tersebut adalah 84 gram.

Jadi, jawaban yang tepat adalah 84.

2.  Subtopik : Kemampuan Nalar pada Bilangan

Level Kognitif : HOTS

Perhatikan teks berikut!

Di sebuah peternakan ayam petelur, ayam-ayam yang diternak dibagi ke dalam 3 kelompok berbeda. Telur-telur dari ayam pada kelompok 1, 2, dan 3 secara berurutan dikumpulkan setiap 3 hari sekali, 4 hari sekali, dan 6 hari sekali. Dalam sekali pengambilan, rata-rata banyak telur yang dapat dikumpulkan dari ayam pada kelompok 1, 2, dan 3 secara berurutan adalah 100 butir telur, 150 butir telur, dan 225 butir telur.

Dalam 12 hari, perkiraan banyak telur yang dapat dikumpulkan dari ayam pada ketiga kelompok adalah … butir telur.

A. 2.250
B. 1.300
C. 950
D. 825
E. 475

 

Kunci Jawaban : B

Pembahasan :

Langkah pertama: Hitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada kelompok 1 dalam 12 hari.

Telur ayam pada kelompok 1 diambil setiap 3 hari sekali dan rata-rata dapat dikumpulkan 100 butir telur dalam sekali pengambilan. Oleh karena itu, dalam 12 hari, telur ayam pada kelompok 1 diambil sebanyak kali. Dengan demikian, perkiraan banyak telur yang dapat dikumpulkan adalah 100 × 4 = 400 butir telur.

Langkah kedua: Hitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada kelompok 2 dalam 12 hari.

Telur ayam pada kelompok 2 diambil setiap 4 hari sekali dan rata-rata dapat dikumpulkan 150 butir telur dalam sekali pengambilan. Oleh karena itu, dalam 12 hari, telur ayam pada kelompok 2 diambil sebanyak kali. Dengan demikian, perkiraan banyak telur yang dapat dikumpulkan adalah 150 × 3 = 450 butir telur.

Langkah ketiga: Hitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada kelompok 3 dalam 12 hari.

Telur ayam pada kelompok 3 diambil setiap 6 hari sekali dan rata-rata dapat dikumpulkan 225 butir telur dalam sekali pengambilan. Oleh karena itu, dalam 12 hari, telur ayam pada kelompok 3 diambil sebanyak kali. Dengan demikian, perkiraan banyak telur yang dapat dikumpulkan adalah 225 × 2 = 450 butir telur.

Langkah keempat: Hitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada ketiga kelompok dalam 12 hari.

Dalam 12 hari, perkiraan banyak telur yang dapat dikumpulkan dari kelompok 1, 2, dan 3 secara berurutan adalah 400, 450, dan 450 butir telur. Dengan demikian, perkiraan banyak telur yang dapat dikumpulkan dari ayam pada ketiga kelompok dalam 12 hari adalah 400 + 450 + 450 = 1. 300 butir telur.

Analisis pilihan jawaban yang salah

• Pilihan jawaban A, yaitu 2.250, bukan merupakan pilihan jawaban yang tepat. Kesalahan utama dalam perhitungan terjadi saat menghitung perkiraan banyak telur yang dapat dikumpulkan dari ayam pada masing-masing kelompok yang seharusnya mengalikan banyak telur yang dikumpulkan dalam sekali pengumpulan dengan banyak pengambilan, tetapi justru mengalikan banyak telur yang dikumpulkan dalam sekali pengumpulan dengan durasi jeda antar pengambilan telur, yaitu 100 × 3 + 150 × 4 + 225 × 6 = 2. 250.
• Pilihan jawaban C, yaitu 950, bukan merupakan pilihan jawaban yang tepat. Kesalahan utama dalam perhitungan adalah menganggap bahwa telur diambil sebanyak 2 kali saja (didapat dari 12 hari yang dibagi dengan jeda waktu terlama antar pengambilan telur, yaitu 6 hari). Oleh karena itu, perhitungannya justru menjadi 2 × (100 + 150 + 225) = 950.
• Pilihan jawaban D, yaitu 825, bukan merupakan pilihan jawaban yang tepat. Kesalahan utama dalam perhitungan adalah dengan menganggap tidak ada pengambilan telur di hari ke-12 sehingga banyak pengambilan telur dari masing-masing kelompok berkurang 1. Banyak pengambilan telur di kelompok 1 menjadi 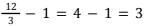kali, banyak pengambilan telur di kelompok 2 menjadi 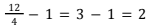kali, dan banyak pengambilan telur di kelompok 3 menjadi 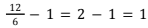kali. Oleh karena itu, perhitungannya justru menjadi 100 × 3 + 150 × 2 + 225 × 1 = 825.
• Pilihan jawaban E, yaitu 475, bukan merupakan pilihan jawaban yang tepat. Kesalahan utama dalam perhitungan adalah menganggap bahwa telur diambil sebanyak 1 kali saja. Oleh karena itu, perhitungannya justru menjadi 100 + 150 + 225 = 475.

Jadi, jawaban yang tepat adalah B.

3. Subtopik : Kemampuan Nalar pada Bilangan

Level Kognitif : HOTS

Perhatikan ilustrasi berikut!

Lantai sebuah aula yang berbentuk persegi akan dipasang keramik berwarna putih dan keramik berwarna hitam dengan pola sebagai berikut.

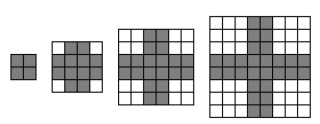
Jika perbandingan banyak keramik putih dan hitam adalah 81: 19, total banyak keramik (hitam dan putih) di aula tersebut adalah … ubin keramik.

Catatan: Tidak ada keramik yang dipotong

A. 100
B. 200
C. 400
D. 500
E. 600

 

Kunci Jawaban : C

Pembahasan :

Diketahui lantai aula berbentuk persegi yang akan dipasangi keramik-keramik berwarna putih dan hitam. Berdasarkan gambar, pola pertama memiliki dimensi ukuran 2 × 2, pola kedua 4 × 4, dan seterusnya.

Berdasarkan informasi pada soal, dapat diperhatikan bahwa untuk aula berdimensi n × n, banyak keramik putih akan mengikuti rumus berikut.

Jika banyak keramik putih adalah , maka banyak keramik hitamnya adalah total keramik dikurang banyak keramik putih, yakni

Diketahui perbandingan banyak keramik putih dan hitam 81: 19. Akibatnya, akan diperoleh perhitungan berikut.

Diperoleh , tetapi karena n menyatakan banyaknya keramik, maka nilai n harus bernilai bulat. Oleh karena itu, diperoleh nilai n yang memenuhi adalah n = 20.

Dengan demikian, total banyak keramik (hitam dan putih) di aula tersebut adalah

Jadi, jawaban yang tepat adalah C.

4. Perhatikan ilustrasi berikut untuk menjawab soal nomor 1-3!

Anggun membawa tiga buah barang, yaitu A, B, dan C yang beratnya berturut-turut   1.450 g, 0,5 kg, dan 3,2 kg ke WahAda Cargo untuk dikirimkan ke Cimahi. Berikut ini tabel yang menunjukkan biaya pengiriman barang.

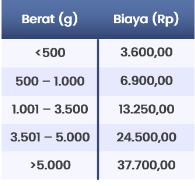
Jika Anggun ingin berhemat, yang paling menguntungkan bagi Anggun di antara pilihan berikut ini adalah …

1. Pengiriman barang A, B, dan C masing-masing terpisah.
2. Pengiriman barang A dan B digabung, sedangkan barang C terpisah.
3. Pengiriman barang A dan C digabung, sedangkan barang B terpisah.
4. Pengiriman barang B dan C digabung, sedangkan barang A terpisah.
5. Pengiriman barang A, B, dan C digabung.

 

Jawaban: B

Pembahasan:

Diketahui bahwa barang A seberat 1.450 g barang B seberat 0,5 kg = 500 g dan barang C seberat 3,2 g = 3.200 g.

Untuk mengetahui pilihan yang paling menguntungkan, akan diperiksa biaya yang dikeluarkan pada setiap pilihan jawaban yang diberikan.

Pilihan jawaban A: Pengiriman barang A, B, dan C masing-masing terpisah.

Karena ketiga barang dikirim terpisah, maka total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang A + biaya barang B + biaya barang C

= 13.250 + 6.900 + 13.250

= 33.400

Didapat bahwa biaya pengiriman pada pilihan A adalah Rp33.400,00.

Pilihan jawaban B: Pengiriman barang A dan B digabung, sedangkan barang C terpisah.

Karena barang A digabung dengan barang B, maka beratnya menjadi 1.450g + 500g = 1.950g. Kemudian total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang A + biaya barang B + biaya barang C

= 13.250 + 13.250

= 26.500

Didapat bahwa biaya pengiriman pada pilihan B adalah Rp26.500,00.

Pilihan jawaban C: Pengiriman barang A dan C digabung, sedangkan barang B terpisah.

Karena barang A digabung dengan barang C, maka beratnya menjadi 1.450g + 3.200g = 4.650g. Kemudian, total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang A dan C + biaya barang B 

= 24.500 + 6.900

= 31.400

Didapat bahwa biaya pengiriman pada pilihan C adalah Rp31.400,00.

Pilihan D: Pengiriman barang B dan C digabung, sedangkan barang A terpisah.

Karena barang B digabung dengan barang C, maka beratnya menjadi 500g + 3.200g = 3.700g. Maka, total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang B dan C + biaya barang A

= 24.500 + 13.250

= 37.750

Didapat bahwa biaya pengiriman pada pilihan D adalah Rp37.750,00.

Pilihan E: Pengiriman barang A, B, dan C digabung.

Karena semua barang digabung, maka beratnya menjadi 1.450g + 500g + 3.200g = 5.150g.  Kemudian, total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang ABC

= 37.700

Didapat bahwa biaya pengiriman pada pilihan E adalah Rp37.700,00.

Berdasarkan perhitungan tersebut, biaya paling murah adalah Rp26.500,00.

Dengan demikian, jika Anggun ingin berhemat, yang paling menguntungkan bagi Anggun adalah pengiriman barang A dan B digabung, sedangkan barang C terpisah.

Jadi, jawaban yang benar adalah B.

5. Diketahui terdapat penambahan biaya pengemasan sebesar Rp3.000,00 untuk setiap pengiriman. Jika Anggun ingin mengirim dua barang sekaligus dan satu barang terpisah, biaya termurah yang dikeluarkan Anggun adalah..

1. Rp44.650,00
2. Rp43.750,00
3. Rp37.400,00
4. Rp32.500,00
5. Rp20.150,00

Jawaban: D

Pembahasan:

Diketahui bahwa barang A seberat 1.450 g barang B seberat 0,5 kg = 500 g dan barang C seberat 3,2 g = 3.200 g.

Diketahui pula terdapat penambahan biaya pengemasan sebesar Rp3.000,00 untuk setiap pengiriman.

Untuk mengetahui total biaya termurah yang dikeluarkan oleh Anggun, akan diperiksa biaya yang dikeluarkan untuk setiap kemungkinan berikut.

Kemungkinan 1: Pengiriman barang A dan B digabung, sedangkan barang C terpisah.

Karena barang A digabung dengan barang B, maka beratnya menjadi 1.450g + 500g = 1.950g. Total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= Biaya barang A dan B + biaya barang C + 2 x biaya pengemasan

= 13.250 + 13.250 + 3.000 x 2

= 26.500 + 6.000

= 32.500

Didapat bahwa biaya yang dikeluarkan Anggun pada kemungkinan 2 adalah Rp 32.500,00.

Kemungkinan 2: Pengiriman barang A dan C digabung, sedangkan barang B terpisah.

Karena barang A digabung dengan barang C, maka beratnya menjadi 1.450g + 3.200g = 4.650g. Total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= Biaya barang A dan C + biaya barang B + 2 x biaya pengemasan

= 24.500 + 6.900 + 3.000 x 2

= 31.400 + 6.000

= 37.400

Didapat bahwa biaya yang dikeluarkan Anggun pada kemungkinan 1 adalah Rp37.400,00.

Kemungkinan 3: Pengiriman barang B dan C digabung, sedangkan barang A terpisah.

Karena barang B digabung dengan barang C, maka beratnya menjadi 500g + 3.200g = 3.700g. Total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= Biaya barang B dan C + biaya barang A + 2 x biaya pengemasan

= 24.500 + 13.250 + 3000 x 2

= 37.750 + 6.000

= 43.750

Didapat bahwa biaya yang dikeluarkan Anggun pada kemungkinan 3 adalah Rp 43.750,00.

Berdasarkan ketiga kemungkinan tersebut, biaya termurah yang dikeluarkan Anggun adalah Rp32.500,00.

Jadi, jawaban yang benar adalah D.

6. Jika terdapat penambahan biaya pengemasan sebesar Rp3.000,00 untuk setiap pengiriman, pilihan berikut yang paling tidak menguntungkan bagi Anggun adalah …

1. Pengiriman barang A, B, dan C digabung.
2. Pengiriman barang A, B, dan C masing-masing terpisah.
3. Pengiriman barang A dan C digabung, sedangkan barang B terpisah.
4. Pengiriman barang A dan B digabung, sedangkan barang C terpisah.
5. Pengiriman barang B dan C digabung, sedangkan barang A terpisah.

Jawaban: E

Pembahasan:

Diketahui bahwa barang A seberat 1.450 g barang B seberat 0,5 kg = 500 g dan barang C seberat 3,2 g = 3.200 g.

Untuk mengetahui pilihan yang paling tidak menguntungkan, akan diperiksa biaya yang dikeluarkan pada setiap pilihan jawaban yang diberikan.

Pilihan jawaban A: Pengiriman barang A, B, dan C digabung.

Karena semua barang digabung, maka beratnya menjadi 1.450g + 500g + 3.200g = 5.150g. Kemudian, total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= Biaya gabungan barang A, B, dan C + biaya pengemasan

= 37.700 + 3.000

= 40.700

Didapat bahwa biaya pengiriman pada pilihan A adalah Rp40.700,00.

Pilihan jawaban B: Pengiriman barang A, B, dan C masing-masing terpisah.

Karena ketiga barang dikirim terpisah, maka total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang A + biaya barang B + biaya barang C + 3 x biaya pengemasan

= 13.250 + 6.900 + 13.250 + 3000 x 3

= 33.400 + 9.000

= 42.400

Didapat bahwa biaya pengiriman pada pilihan B adalah Rp42.400,00.

Pilihan jawaban C: Pengiriman barang A dan C digabung, sedangkan barang B terpisah.

Karena barang A digabung dengan barang C, maka beratnya menjadi 1.450g + 3.200g = 4.650g. Kemudian, total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang A dan C + biaya barang B + 2 x biaya pengemasan

= 24.500 + 6.900 + 3000 x 2

= 31.400 + 6.000

= 37.400

Didapat bahwa biaya pengiriman pada pilihan C adalah Rp37.400,00.

Pilihan jawaban D: Pengiriman barang A dan B digabung, sedangkan barang C terpisah.

Karena barang A digabung dengan barang B, maka beratnya menjadi 1.450g + 500g = 1.950g. Kemudian, total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang A dan B + biaya barang C + 2 x biaya pengemasan

= 13.250 + 13.250 + 3000 x 2

= 26.500 + 6.000

= 32.500

Didapat bahwa biaya pengiriman pada pilihan D adalah Rp32.500,00.

Pilihan jawaban E: Pengiriman barang B dan C digabung, sedangkan barang A terpisah. 

Karena barang B digabung dengan barang C, maka beratnya menjadi 500g + 3.200g = 3.700g.  Kemudian, total biaya yang dikeluarkan adalah sebagai berikut.

Total biaya

= biaya barang B dan C + biaya barang A + 2 x biaya pengemasan

= 24.500 + 13.250 + 3000 x 2

= 37.750 + 6.000

= 43.750

Didapat bahwa biaya pengiriman pada pilihan E adalah Rp43.750,00.

Berdasarkan perhitungan tersebut, biaya yang paling mahal adalah Rp43.750,00.

Dengan demikian, pilihan yang paling tidak menguntungkan bagi Anggun adalah pengiriman barang B dan C digabung, sedangkan barang A terpisah.

Jadi, jawaban yang benar adalah E.

7. Perhatikan informasi berikut untuk menjawab soal nomor 4 dan 5!

Faktor-faktor yang memengaruhi terjadinya reaksi kimia adalah perubahan energi Gibbs , perubahan entalpi , perubahan entropi , dan temperatur  dalam satuan Kelvin. Persamaan matematisnya adalah sebagai berikut.

Reaksi terjadi jika perubahan energi Gibbs bernilai negatif. Syarat reaksi yang bisa terjadi pada suhu 127 Celcius adalah ….

Jawaban: C

Pembahasan:

Diketahui persamaan berikut.

Karena syarat reaksi terjadi adalah perubahan energi Gibbs bernilai negatif, maka didapat pertidaksamaan berikut.

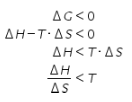
Berdasarkan informasi pada soal, variabel T harus dalam satuan Kelvin. Oleh karena itu, suhu 127 Celcius pada soal perlu diubah ke dalam satuan Kelvin.

Ingat bahwa konversi derajat Celcius ke Kelvin adalah penambahan 273 sehingga didapat perhitungan berikut.

T = 127 C

= 127 + 273

= 400 K

Akibatnya, pertidaksamaan sebelumnya dapat ditulis menjadi seperti berikut.

Pertidaksamaan tersebut memiliki arti bahwa kurang dari 400.

Ingat bahwa makna “kurang dari” berbeda dengan “tidak lebih dari”. Pada frasa “kurang dari 400”, angka 400 tidak termasuk dalam penyelesaian, sedangkan pada frasa “tidak lebih dari 400”, angka 400 masuk dalam penyelesaian.

Dengan demikian, syarat reaksi yang bisa terjadi pada suhu 127 Celcius adalah kurang dari 400.

8. Reaksi terjadi jika perubahan energi Gibbs bernilai negatif. Jika suatu reaksi memiliki sebesar dan sebesar dengan a > 0 dan b > 0.  Temperatur yang dibutuhkan agar reaksi dapat terjadi adalah ….

Jawaban: E

Pembahasan:

Diketahui persamaan berikut.

Karena syarat reaksi terjadi adalah perubahan energi Gibbs bernilai negatif, maka didapat pertidaksamaan berikut.

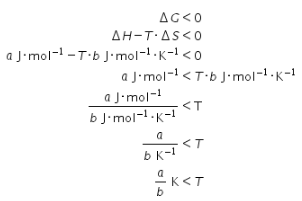Dengan demikian, temperatur yang dibutuhkan agar reaksi dapat terjadi adalah .

Maka, jawaban yang benar adalah E.

Baca juga: Soal Terbaru Tes Potensi Kognitif dan Pembahasannya

9. Pajak Penghasilan (PPh) berdasarkan UU PPh didefinisikan sebagai pajak yang dikenakan kepada orang pribadi atau badan atas penghasilan yang diperoleh dalam tahun pajak. Untuk Penghasilan Tidak Kena Pajak (PTKP), karyawan yang memiliki status belum menikah dan tidak memiliki tanggungan adalah Rp54.000.000,00 per tahun. PPh termasuk ke dalam pajak progresif sehingga tarif pajak yang akan makin naik sesuai dengan naiknya dasar pengenaan pajak. Diketahui perhitungan tarif PPh berdasarkan pasal 21 sesuai UU PPh didasari oleh Penghasilan Kena Pajak (PKP) dan disajikan dalam tabel berikut.

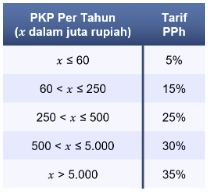
Sebagai contoh, untuk penghasilan Andi setelah dikurangi PTKP adalah Rp300.000.000,00 per tahun, maka dikenakan tarif pajak sampai lapis ketiga, yaitu 25%. Pada tarif lapis pertama, Rp60.000.000,00 pertama dikenakan tarif pajak 5%. Kemudian, pada tarif lapis kedua, Rp190.000.000,00 berikutnya (dari 60 juta sampai 250 juta) dikenakan tarif pajak 15%. Selanjutnya, pada tarif lapis terakhir, sisa Rp50.000,000 dikenakan tarif pajak 25%.

Nisa adalah seorang karyawan tetap di suatu perusahaan dengan status belum menikah dan tidak memiliki tanggungan dengan penghasilan netto sebesar Rp42.500.000,00 per bulan. Persentase tarif PPh progresif yang dikenakan kepada Nisa adalah sampai ….

1. 5%
2. 15%
3. 25%
4. 30%
5. 35%

 

Jawaban: C

Pembahasan:

Misalkan penghasilan Nisa selama 1 tahun adalah P, maka besarnya dalam setahun yaitu sebagai berikut.

P = Rp 42.500.000,00 x 12

P = Rp 510.000.000,00

Misalkan penghasilan kena pajak Nisa sebesar , maka karena Nisa belum menikah dan tidak memiliki tanggungan, PTKPnya sebesar Rp54.000.000,00, sehingga besarnya penghasilan Nisa yang kena pajak yaitu sebagai berikut.

= P – 54.000.000,00

= 510.000.000, 00 – 54.000.000,00

= 456.000.000,00

Dengan membandingkan dengan tabel yang diberikan dalam soal, maka penghasilan kena pajak Nisa akan dikenakan tarif progresif sebesar 25%.

Jadi, jawaban yang benar adalah C.

10. Perhatikan gambar berikut ini!

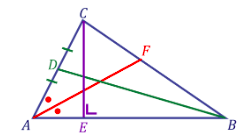
Terdapat garis istimewa pada sebuah segitiga, yaitu garis tinggi, garis bagi, dan garis berat dengan definisi masing-masing garis sebagai berikut.

• Garis tinggi adalah garis lurus yang menghubungkan salah satu titik sudut segitiga ke sisi di hadapannya secara tegak lurus.

• Garis bagi adalah garis yang dibuat dari salah satu titik sudut segitiga dan membagi sudut tersebut menjadi dua bagian sama besar.

• Garis berat adalah garis yang menghubungkan salah satu titik sudut segitiga ke sisi di hadapannya dan membagi sisi tersebut menjadi dua bagian sama panjang.

   

   

Jika salah satu sisi adalah garis tinggi dan salah satu garis bagi juga berperan sebagai garis berat, jenis segitiga yang dimaksud adalah ….

1. segitiga siku-siku sama kaki 
2. segitiga sembarang
3. segitiga sama kaki
4. segitiga sama sisi
5. segitiga siku-siku

Jawaban: A

Pembahasan:

Segitiga yang dimaksud memiliki kriteria sebagai berikut.

• Salah satu sisi adalah garis tinggi.

• Salah satu garis bagi adalah garis berat.

Garis tinggi adalah garis tegak lurus yang menghubungkan salah satu titik sudut segitiga ke salah satu sisi segitiga.

Diketahui salah satu sisi merupakan garis tinggi. Akibatnya, terdapat dua sisi segitiga yang saling tegak lurus. Segitiga dengan kriteria ini adalah segitiga siku-siku.

Kemudian, diketahui salah satu garis bagi juga berperan sebagai garis berat. Garis bagi membagi sudut sama besar, sedangkan garis berat membagi sisi sama panjang.

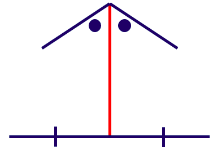
Kesimpulan sebelumnya menyatakan bahwa segitiga yang dimaksud merupakan segitiga siku-siku. Sudut siku-siku yang mungkin adalah sudut yang dibagi oleh garis bagi yang ditandai warna merah.

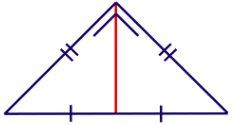
Dengan demikian, segitiga yang dimaksud adalah segitiga siku-siku sama kaki.

Jadi, jawaban yang benar adalah A.

11. Tujuh buah silinder dengan jari-jari 7 cm disusun dan dibungkus sehingga membentuk tampak atas seperti gambar berikut.

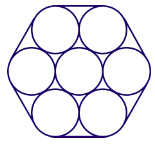Jika volume total silinder sebesar 10.780 cm³, volume antar ruang yang terbentuk sebesar ….

Catatan: Gunakan

Jawaban: A

Pembahasan:

Gambar pada soal dapat dibuat garis bantu seperti gambar berikut.

 

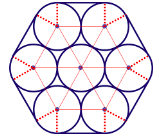
Gambar dapat disimpulkan terbentuk dari komponen-komponen berikut.

• Sigitiga samasisi dengan ukuran sisi 2r sebanyak 6 buah.
• Persegi panjang dengan ukuran 2r x r sebanyak 6 buah.
• Enam buah juring lingkaran yang membentuk 1 lingkaran.

Luas penampang dapat dihitung dengan persamaan berikut.

Tinggi bangun ruang sama besar dengan tinggi silinder. Berdasarkan volume total dan dimensi alas silinder, tinggi silinder dapat ditentukan dengan persamaan berikut.

Volume total bangun ruang akan memenuhi persamaan berikut.

Dengan demikian, volume antar ruang dari bangun yang dimaksud sebesar

Jadi, jawaban yang benar adalah A.

12. Berdasarkan perspektif ekonomi, usia penduduk dikategorikan menjadi dua bagian, yaitu usia produktif (15—59 tahun) dan usia tidak produktif (di bawah 15 tahun dan 60 tahun ke atas). Jumlah penduduk pada suatu negara tahun 2021 tercatat sebagai berikut.

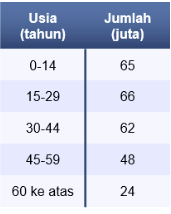
Persentase penduduk yang berada pada kategori usia tidak produktif di negara tersebut adalah sekitar ….

1. 9,05%
2. 24,52%
3. 33,58%
4. 42,25%
5. 66,67%

 

Jawaban: C

Pembahasan:

Berdasarkan informasi pada soal, kategori penduduk tidak produktif meliputi kelompok usia di bawah 15 tahun dan 60 tahun ke atas. Oleh karena itu, jumlah penduduk dari kedua kelompok usia tersebut adalah sebagai berikut.

n (tidak produktif) = 65 + 24

                               = 89

Sementara itu, jumlah seluruh penduduk di negara tersebut adalah sebagai berikut.

n (total) = 65 + 66 + 62 + 48 +24

              = 265

Persentase penduduk dengan kategori usia tidak produktif dapat dihitung sebagai berikut.

Dengan demikian, persentase penduduk yang berada pada usia tidak produktif adalah sekitar 33,58%.

Jadi, jawaban yang benar adalah C.

Baca juga: Contoh Soal Literasi Bahasa Inggris SNBT/UTBK 2023

13. Permintaan jastip atau jasa titip cukup tinggi di Indonesia, salah satunya dalam hal pembelian tiket konser. Rani, seorang penggemar K-pop, ingin membeli tiket konser untuk pertama kalinya. Karena takut gagal jika membeli sendiri, Rani memutuskan menggunakan jastip. Ia membandingkan beberapa akun jastip pembelian tiket untuk mengetahui kemungkinan keberhasilannya. Berikut data hasil perbandingannya.

Dari data tersebut, pernyataan yang BENAR adalah … 

Catatan: Jawaban bisa lebih dari satu

1. Persentase keberhasilan akun A lebih besar dari akun B.
2. Persentase keberhasilan akun C lebih kecil dari akun D.
3. Persentase keberhasilan akun E lebih kecil dari akun F.
4. Persentase keberhasilan akun E bukanlah yang paling besar.
5. Persentase keberhasilan akun D adalah yang paling kecil.

Jawaban:

Pernyataan yang bernilai BENAR adalah Persentase keberhasilan akun C lebih kecil dari akun D dan Persentase keberhasilan akun E bukanlah yang paling besar.

Pembahasan:

Kita dapat menggunakan rumus peluang empiris untuk mencari empat akun dengan peluang keberhasilan tertinggi. Peluang empiris dapat dinotasikan dengan rumus berikut ini.

Berdasarkan rumus tersebut, kita perlu menghitung peluang keberhasilan akun dalam pembelian tiket konser dengan membandingkan antara banyaknya transaksi pembelian tiket yang berhasil dengan banyaknya transaksi yang dilakukan. Jika dilakukan perhitungan terhadap dua besaran tersebut, akan diperoleh hasil seperti pada tabel berikut.

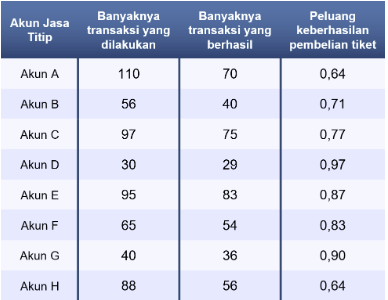
Kemudian, akan diperiksa setiap pernyataan yang ada di pilihan jawaban sebagai berikut.

Persentase keberhasilan akun A lebih besar dari akun B.

Dari tabel tersebut diperoleh persentase keberhasilan akun A lebih kecil dari akun B. Oleh karena itu, pernyataan bernilai SALAH.

Persentase keberhasilan akun C lebih kecil dari akun D.

Dari tabel tersebut diperoleh persentase keberhasilan akun C lebih kecil dari akun D. Oleh karena itu, pernyataan bernilai BENAR.

Persentase keberhasilan akun E lebih kecil dari akun F.

Dari tabel tersebut diperoleh persentase keberhasilan akun E lebih besar dari akun F. Oleh karena itu, pernyataan bernilai SALAH.

Persentase keberhasilan akun E bukanlah yang paling besar.

Dari tabel tersebut diperoleh persentase keberhasilan paling besar adalah akun D sehingga persentase keberhasilan akun E bukanlah yang paling besar. Oleh karena itu, pernyataan bernilai BENAR.

Persentase keberhasilan akun D adalah yang paling kecil.

Dari tabel tersebut diperoleh persentase keberhasilan paling kecil adalah akun A dan akun H. Oleh karena itu, pernyataan bernilai SALAH.

Jadi, jawaban yang benar adalah B dan D.

 

14. Perhatikan ilustrasi berikut!

Gedung Teater

Dalam suatu gedung teater di Provinsi Suka-Suka terdapat 11 baris kursi. Baris pertama berisi 10 kursi, baris kedua berisi 15 kursi, baris ketiga berisi 17 kursi, baris keempat berisi 22 kursi, baris ke lima berisi 24 kursi, dan seterusnya mengikuti pola yang sama. Berdasarkan informasi tersebut, banyaknya kursi pada baris kedua dari belakang adalah … kursi.

1. 31
2. 36
3. 38
4. 43
5. 45

 

Jawaban: D

Pembahasan:

Pola susunan kursi pada gedung teater tersebut dapat diuraikan sebagai berikut.

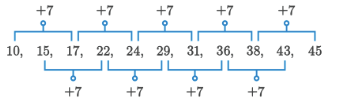
Berdasarkan pola tersebut, dapat disimpulkan bahwa banyaknya kursi yang berada pada baris kedua dari belakang atau baris kesepuluh adalah 43 kursi.

Jadi, jawaban yang tepat adalah D.

15. Perhatikan ilustrasi berikut!

Gedung Teater

Dalam suatu gedung teater di Provinsi Suka-Suka terdapat 11 baris kursi. Baris pertama berisi 10 kursi, baris kedua berisi 15 kursi, baris ketiga berisi 17 kursi, baris keempat berisi 22 kursi, baris ke lima berisi 24 kursi, dan seterusnya mengikuti pola yang sama.

Sekelompok siswa SMA menonton pertunjukan di gedung teater tersebut dan memilih duduk di dua baris paling akhir. Apabila seluruh siswa tersebut duduk tepat di satu kursi dan tidak ada kursi yang kosong pada dua baris paling akhir, maka banyaknya siswa SMA yang menonton pertunjukan tersebut adalah … siswa.

1. 71
2. 75
3. 81
4. 85
5. 88

 

Jawaban: E

Pembahasan:

Diketahui seluruh siswa duduk tepat di satu kursi dan tidak ada kursi yang kosong pada dua baris paling akhir. Artinya, banyaknya siswa SMA yang menonton pertunjukan tersebut sama dengan banyaknya kursi pada dua baris paling akhir.

Pola susunan kursi pada gedung teater tersebut dapat diuraikan sebagai berikut.

Berdasarkan pola tersebut, dapat disimpulkan bahwa jumlah kursi yang terdapat pada dua baris terakhir, yaitu baris ke-10 dan ke-11 adalah 43 dan 45. Oleh karena itu, total banyaknya kursi yang terdapat pada dua baris paling akhir tersebut adalah 43 + 45 = 88 kursi. Dengan demikian, banyaknya siswa SMA yang menonton pertunjukan tersebut adalah 88 siswa.

Jadi, jawaban yang tepat adalah E.

16. Perhatikan ilustrasi berikut!

Gedung Teater

Dalam suatu gedung teater di Provinsi Suka-Suka terdapat 11 baris kursi. Baris pertama berisi 10 kursi, baris kedua berisi 15 kursi, baris ketiga berisi 17 kursi, baris keempat berisi 22 kursi, baris ke lima berisi 24 kursi, dan seterusnya mengikuti pola yang sama.

Apabila dalam suatu pertunjukan teater hanya terisi setengah dari total kapasitas gedung, maka banyaknya kursi yang kosong dalam gedung teater tersebut adalah ….

1. 310
2. 255
3. 155
4. 85
5. 75
   

Jawaban: C

Pembahasan: 

Pola susunan kursi pada gedung teater tersebut dapat diuraikan sebagai berikut.

Berdasarkan pola tersebut, dapat diketahui beberapa informasi berikut ini.

• Total kursi yang terdapat pada gedung teater adalah sebagai berikut.

Total kursi = 10 + 15 + 17 + 22 + 24 + 29 + 31 + 36 + 38 + 43 + 45

                  = 310

• Jika hanya setengah dari kapasitas gedung yang terisi, maka banyaknya kursi yang kosong adalah sebagai berikut.

Banyaknya kursi kosong  = 1/2  x  310

                                         = 155

Dengan demikian, banyaknya kursi yang kosong adalah 155 kursi.

Jadi, jawaban yang tepat adalah C.

Baca juga: Contoh Soal Literasi Bahasa Indonesia SNBT/UTBK 2023

17. Perhatikan ilustrasi berikut!

Gedung Teater

Dalam suatu gedung teater di Provinsi Suka-Suka terdapat 11 baris kursi. Baris pertama berisi 10 kursi, baris kedua berisi 15 kursi, baris ketiga berisi 17 kursi, baris keempat berisi 22 kursi, baris ke lima berisi 24 kursi, dan seterusnya mengikuti pola yang sama.

Apabila dalam suatu pertunjukan teater hanya terisi setengah dari total kapasitas gedung dan harga tiket pertunjukan adalah Rp30.000,00 per orang, total pendapatan dari pertunjukan tersebut adalah ….

1. Rp9.300.000,00
2. RP6.975.000,00
3. Rp4.650.000,00
4. Rp3.650.000,00
5. Rp2.325.000,00

 

Jawaban: C

Pembahasan: 

Pola susunan kursi pada gedung teater tersebut dapat diuraikan sebagai berikut.

Berdasarkan pola tersebut, dapat diketahui beberapa informasi berikut ini.

• Total kursi yang terdapat pada gedung teater adalah sebagai berikut.

Total kursi = 10 + 15 + 17 + 22 + 24 + 29 + 31 + 36 + 38 + 43 + 45

                  = 310

• Jika hanya setengah dari kapasitas gedung yang terisi, maka banyaknya kursi yang terisi adalah sebagai berikut.

Banyaknya kursi yang terisi  = 1/2 x 310

                                               = 155

• Total pendapatan dari teater di hari tersebut adalah sebagai berikut.

Total pendapatan = banyaknya kursi yang terisi harga tiket

                            = 155 x Rp30.000,00

                            = Rp4.650.000,00

Dengan demikian, total pendapatan yang diperoleh dari pertunjukan teater di hari tersebut adalah Rp4.650.000,00.

Jadi, jawaban yang tepat adalah C.

18. Perhatikan ilustrasi berikut!

Premi Asuransi Kesehatan

Dua orang karyawan swasta mendaftar sebagai peserta asuransi kesehatan dengan besar premi yang sama. Guna membayar premi asuransi tersebut, karyawan A yang memiliki gaji Rp6.000.000,00 akan dikenakan potongan gaji sebesar 4%, sedangkan karyawan B dikenakan potongan gaji sebesar 6%.

Berdasarkan informasi tersebut, besar gaji karyawan B adalah ….

1. Rp5.000.000,00
2. Rp5.500.000,00
3. Rp4.500.000,00
4. Rp4.000.000,00
5. Rp3.500.000,00

 

Jawaban: D

Pembahasan: 

Misalkan X menyatakan besar gaji karyawan B.

Diketahui premi asuransi karyawan A sama dengan karyawan B. Oleh karena itu, didapat perhitungan sebagai berikut.

Premi asuransi karyawan A = Premi asuransi karyawan B

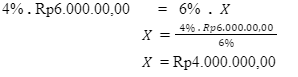
Dengan demikian, besarnya gaji karyawan B adalah Rp4.000.000,00

Jadi, jawaban yang tepat adalah D.

19. Perhatikan ilustrasi berikut!

Premi Asuransi Kesehatan

Dua orang karyawan swasta mendaftar sebagai peserta asuransi kesehatan dengan besar premi yang sama. Guna membayar premi asuransi tersebut, karyawan A yang memiliki gaji Rp6.000.000,00 akan dikenakan potongan gaji sebesar 4%, sedangkan karyawan B dikenakan potongan gaji sebesar 6%.

Pernyataan yang tepat berkaitan dengan informasi tersebut adalah …

1. Sisa gaji karyawan A setelah dipotong premi asuransi adalah Rp5.670.000,00.
2. Sisa gaji karyawan B setelah dipotong premi asuransi adalah Rp3.870.000,00.
3. Premi asuransi karyawan A dan karyawan B masing-masing adalah Rp230.000,00.
4. Total gaji karyawan A dan B setelah dipotong premi asuransi adalah Rp9.520.000,00.
5. Selisih gaji karyawan A dan B sebelum dipotong premi asuransi adalah Rp1.500.000,00.

 

Jawaban: D

Pembahasan: 

Untuk menjawab soal ini, akan ditentukan terlebih dahulu gaji karyawan B serta besar premi asuransi yang harus dibayarkan oleh karyawan A maupun karyawan B.

Perhatikan beberapa perhitungan berikut.

• Besar gaji karyawan B

Misalkan X menyatakan besar gaji karyawan B. Diketahui premi asuransi karyawan A sama dengan karyawan B. Oleh karena itu, didapat perhitungan sebagai berikut.

Premi asuransi karyawan A  =   Premi asuransi karyawan B

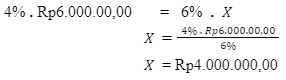
• Besar premi yang harus dibayar oleh karyawan A dan B

Besar premi = Persentase premi asuransi karyawan A gaji karyawan A

                     = 4% x Rp6.000.00,00

                     = Rp240.000,00

Akibatnya, premi asuransi karyawan B juga sebesar Rp240.000,00.

Selanjutnya, akan dianalisis pada setiap pernyataan pada pilihan jawaban yang diberikan.

• Pilihan A: Sisa gaji karyawan A setelah dipotong premi asuransi adalah Rp5.670.000,00. Sisa gaji karyawan A setelah dipotong premi asuransi dapat dihitung sebagai berikut.

         Sisa gaji karyawan A = Gaji karyawan A – Premi asuransi karyawan A

                                            = Rp6.000.000,00 – Rp240.000,00

                                            = Rp5.760.000,00

         Oleh karena itu, pernyataan pada pilihan A tidak tepat.

• Pilihan B: Sisa gaji karyawan B setelah dipotong premi asuransi adalah Rp3.870.000,00. Sisa gaji karyawan B setelah dipotong premi asuransi dapat dihitung sebagai berikut.Sisa gaji karyawan B = Gaji karyawan B – Besar premi asuransi 

                                            = Rp4.0000.000,00 – Rp240.000,00

                                            = Rp3.760.000,00

         Oleh karena itu, pernyataan pada pilihan B tidak tepat.

• Pilihan C: Premi asuransi karyawan A dan karyawan B masing-masing adalah Rp230.000,00.Telah didapatkan pada perhitungan sebelumnya bahwa premi asuransi karyawan A dan karyawan B masing-masing adalah Rp240.000,00.

         Oleh karena itu, pernyataan pada pilihan C tidak tepat.

• Pilihan D: Total gaji karyawan A dan B setelah dipotong premi asuransi adalah Rp9.520.000,00.Total gaji karyawan A dan B setelah dipotong premi asuransi dapat dihitung dengan menjumlah sisa gaji kedua karyawan tersebut setelah dipotong premi asuransi, yakni sebagai berikut.

         Total gaji = Sisa gaji karyawan A + Sisa gaji karyawan B

                         = Rp5.760.000,00 + Rp3.760.000,00

                         = Rp9.520.000,00.

         Oleh karena itu, pernyataan pada pilihan D tepat.

• Pilihan E: Selisih gaji karyawan A dan B sebelum dipotong premi asuransi adalah Rp1.500.000,00.Selisih gaji karyawan A dan B sebelum dipotong premi asuransi dapat dihitung sebagai berikut.Gaji karyawan A – Gaji karyawan B = Rp6.000.000,00 – Rp4.000.000,00

         = Rp2.000.000,00

         Oleh karena itu, pernyataan pada pilihan E tidak tepat.

Jadi, jawaban yang tepat adalah D.

20. Perhatikan teks berikut!

Transmigrasi ke Pulau Kalimantan

Transmigrasi merupakan salah satu upaya pemerintah untuk menyelesaikan masalah ketidakmerataan persebaran penduduk dan pembangunan di wilayah Indonesia. Program transmigrasi sendiri merupakan upaya untuk memindahkan penduduk dari wilayah yang kepadatan penduduknya tinggi ke wilayah yang lebih rendah kepadatannya. Dengan demikian, data kependudukan menjadi salah satu faktor pertimbangan utama dalam program transmigrasi. Salah satu wilayah yang diprioritaskan menjadi wilayah tujuan transmigrasi adalah Pulau Kalimantan yang memiliki kepadatan penduduk cukup rendah. Kepadatan penduduk sendiri merupakan hasil bagi antara jumlah penduduk terhadap luas wilayah. Berikut adalah kondisi kependudukan dari Pulau Kalimantan pada tahun 2019.

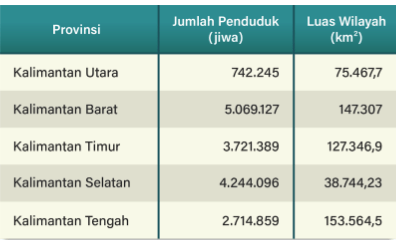
Sumber: BPS

Berdasarkan data tersebut, provinsi di Pulau kalimantan yang akan diprioritaskan untuk menjadi tujuan transmigrasi adalah ….

1. Kalimantan Utara
2. Kalimantan Barat
3. Kalimantan Timur
4. Kalimantan Selatan
5. Kalimantan Tengah

Jawaban: A

Pembahasan: 

Kepadatan penduduk merupakan hasil bagi antara jumlah penduduk terhadap luas wilayah.

Dengan demikian, didapatkan rumus sebagai berikut.

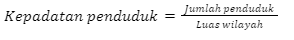
Untuk menjawab soal ini, akan dihitung kepadatan penduduk pada tiap provinsi dengan menggunakan rumus di atas.

Kalimantan Utara

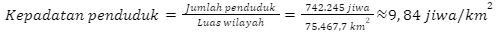
Kalimantan Barat

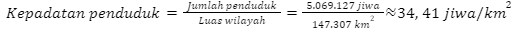
Kalimantan Timur

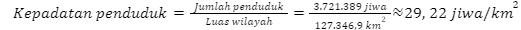
Kalimantan Selatan

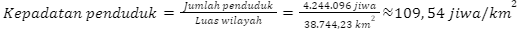
Kalimantan Tengah

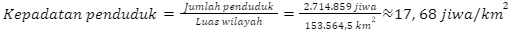
Berdasarkan hasil perhitungan tersebut, dapat disimpulkan bahwa Provinsi di Pulau Kalimantan yang memiliki kepadatan penduduk paling rendah adalah Kalimantan Utara. Dengan kata lain, provinsi di Pulau Kalimantan yang akan diprioritaskan untuk menjadi tujuan transmigrasi adalah Kalimantan Utara.

Jadi, jawaban yang tepat adalah A.

21. Sebuah film berdurasi 1 jam 25 menit 15 detik disimpan pada sebuah CD yang memiliki laju cetak informasi 20.000 data per detik. Jika diketahui setiap data terdiri dari 48 bit, kapasitas penyimpanan yang terpakai pada CD tersebut sebesar …. (1 byte = 8 bit)

1. 3.928,3 Mb
2. 613,8 Mb
3. 491,4 Mb
4. 102,3 Mb
5. 96,6 Mb

 

Jawaban: B

Pembahasan: 

Diketahui:

durasi film = 1 jam 25 menit 15 detik

durasi film = 5.115 detik

laju cetak = 20.000 data/detik

1 data = 48 bit

1 byte = 8 bit

Kapasitas penyimpanan yang terpakai dapat diketahui dengan perhitungan berikut ini.

= durasi film x laju cetak x jumlah bit per data

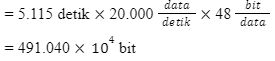
Ubah menjadi satuan byte.

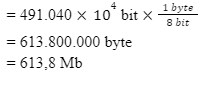
Berdasarkan hasil perhitungan tersebut, dapat diketahui bahwa kapasitas penyimpanan yang terpakai pada CD adalah 613,8 Mb.

Jadi, jawaban yang tepat adalah B.

Baca juga: Contoh Soal Potensi Kognitif SNBT/UTBK 2023

22. Nada sedang menjumlahkan nomor-nomor pada halaman buku miliknya mulai dari halaman 100 sampai halaman 200. Jika jumlah nomor halaman yang didapatkan Nada 15.300, pernyataan yang tepat adalah …

1. Nada menghitung halaman 150 sebanyak dua kali.
2. Nada menghitung halaman 100 dan 50 sebanyak dua kali.
3. Hasil perhitungan Nada sudah tepat dan tidak ada kesalahan.
4. Halaman 150 terlewat oleh Nada sehingga tidak masuk dalam perhitungan.
5. Halaman 100 dan 50 terlewat oleh Nada sehingga tidak masuk dalam perhitungan.

 

Jawaban: A

Pembahasan:

Diketahui:

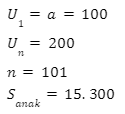
Soal ini dapat dijawab menggunakan rumus jumlah n data pada deret aritmetika berikut ini.

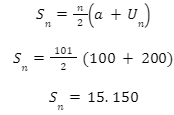
Selisih hasil hitungan Nada dan hasil hitungan dengan rumus adalah sebagai berikut.

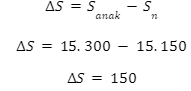
Hasil hitungan Nada lebih besar dibandingkan hasil hitungan dengan rumus, hal ini menandakan bahwa ada halaman yang terhitung dua kali oleh Nada. Hal ini dikarenakan Nada mulai menghitung dari halaman 100 sampai 200. Halaman yang terhitung dua kali oleh Nada adalah halaman 150 sehingga pernyataan A tepat. Berdasarkan hasil perhitungan tersebut, kita juga dapat mengetahui beberapa informasi lainnya

• Pernyataan B tidak tepat, karena halaman 50 tidak ikut dihitung oleh Nada.
• Pernyataan C tidak tepat, karena hasil hitungan Nada tidak sesuai dengan hasil hitungan dengan rumus jumlah n suku pertama deret pertama.
• Pernyataan D tidak tepat, karena hasil hitungan Nada lebih besar sehingga ada halaman yang terhitung dua kali, bukan tidak terhitung.
• Pernyataan E tidak tepat, karena hasil hitungan Nada lebih besar sehingga ada halaman yang terhitung dua kali, bukan tidak terhitung. Kemudian, halaman 50 tidak ada dalam rentang halaman yang dihitung Nada.

Jadi, jawaban yang tepat adalah A.

23. Perhatikan ilustrasi berikut!

Persiapan Acara

Pak Abdul akan mengadakan pesta besar di rumahnya sehingga ia harus membeli berbagai macam bahan kebutuhan pokok. Sebelumnya, ia sudah membeli 20 karung beras dan 6 dus minyak goreng dengan total harga Rp3.600.000,00. Kemudian, Pak Abdul menambah 15 karung beras dan 5 dus minyak goreng dengan total harga Rp2.800.000,00.

Berapakah total pengeluaran Pak Abdul jika keseluruhan kebutuhannya adalah 45 karung beras dan 15 dus minyak goreng?

1. Rp6.400.000,00
2. Rp8.400.000,00
3. Rp10.800.000,00
4. Rp12.560.000,00
5. Rp14.800.000,00

 

Jawaban: B

Pembahasan: 

Misalkan
Harga beras = x

Harga minyak goreng = y

Persamaan yang dibuat berdasarkan ilustrasi tersebut adalah sebagai berikut.

20x + 6y= Rp3.600.000,00

15x + 5y= Rp2.800.000,00

Kemudian, eliminasi kedua persamaan tersebut sebagai berikut.

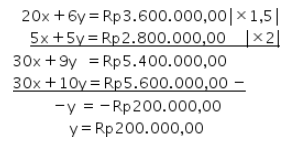
Substitusikan nilai y ke salah satu persamaan, seperti berikut.

Jadi, harga beras per karung Rp120.000,00 dan minyak goreng Rp200.000,00/dus. Total pengeluaran Pak Abdul untuk 45 karung beras dan 15 dus minyak goreng dapat dihitung sebagai berikut.

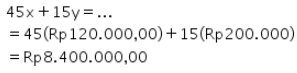
Berdasarkan hasil perhitungan tersebut, dapat diketahui bahwa total pengeluaran Pak Abdul untuk 45 karung beras dan 15 dus minyak goreng adalah Rp8.400.000,00.

Jadi, jawaban yang tepat adalah B.

Untuk kamu yang mau nonton video pembahasan soalnya juga bisa banget nih!

Mau belajar lebih banyak seputar materi dan tryout menjelang SNBT 2024? Yuk, daftar Brain Academy. Kamu bisa datang ke cabang terdekat atau belajar online via aplikasi Ruangguru. Mulai atur strategi bersama konselor dan Master Teacher supaya lolos ke jurusan impian. Semangat!