Contoh Soal Kemampuan Kuantitatif UTBK SNBT 2025

UTBK SNBT semakin dekat. Persiapkan dirimu dengan latihan soal dan pembahasan TPS Kemampuan Kuantitatif 2025 berikut ini!

—

1. Contoh Soal Isian Kemampuan Kuantitatif (NEW!)

Topik : Statistika dan Peluang

Subtopik : Konsep Dasar Statistika Deskriptif

Level Kognitif : MOTS

Diagram batang berikut ini menunjukkan bruto dan neto dari empat jenis produk minuman yang dijual di sebuah toko.

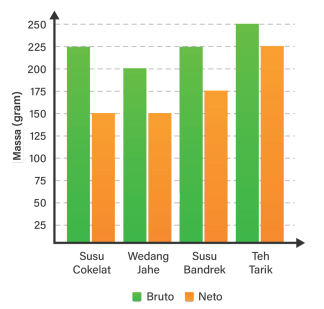
Berdasarkan diagram batang tersebut, rata-rata massa kemasan keempat minuman di atas adalah … gram.

Catatan: Hanya diisi dengan angka (contoh: 10)

 

Kunci Jawaban : 50

Pembahasan :

Besar tara (kemasan) dari setiap produk dapat dihitung dengan cara berikut ini.

● Susu Cokelat

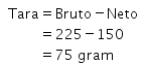
● Wedang Jahe

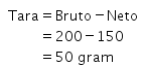
● Susu Bandrek

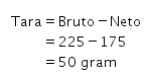
● Teh Tarik

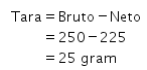
Kemudian, hitung rata-rata tara dari keempat produk tersebut sehingga diperoleh perhitungan berikut ini.

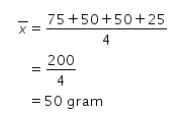
Jadi, jawaban yang tepat adalah 50.

2. Topik : Bilangan

Subtopik : Konsep Dasar Himpunan

Level Kognitif : HOTS

Dalam suatu sekolah dengan total 135 murid, siswa yang menyukai basket, renang, dan kasti masing-masing ada sebanyak 50, 30, dan 45 siswa. Lalu, sebanyak x siswa menyukai basket dan renang, sebanyak y siswa menyukai basket dan kasti, sebanyak z siswa menyukai renang dan kasti, sebanyak p siswa yang tidak menyukai ketiga olahraga tersebut, dan sebanyak q siswa yang menyukai ketiga olahraga tersebut. Diketahui pula bahwa x + y + z = p.

Berdasarkan informasi tersebut, manakah di antara pilihan berikut yang bernilai benar?

1. Banyaknya murid yang menyukai basket, renang, dan kasti adalah 10 orang.
2. Banyaknya murid yang hanya menyukai basket dan renang adalah x − 10 orang.
3. Banyaknya murid yang menyukai renang atau kasti adalah 75 orang.
4. Banyaknya murid yang menyukai tepat dua jenis olahraga adalah x + y + z orang.

 

1. 1, 2, dan 3 SAJA yang benar.
2. 1 dan 3 SAJA yang benar.
3. 2 dan 4 SAJA yang benar.
4. HANYA 4 yang benar.
5. SEMUA pilihan benar.

 

Kunci Jawaban : A

Pembahasan :

Perhatikan Diagram Venn berikut!

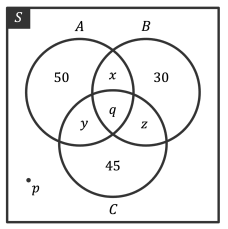
Misalkan himpunan A, B, dan C berturut-turut adalah himpunan siswa yang menyukai basket, renang, dan kasti di sebuah sekolah dengan total murid sebanyak 135 orang. Selain itu, diketahui pula x + y + z = p.

Dari Diagram Venn, diperoleh hubungan sebagai berikut.

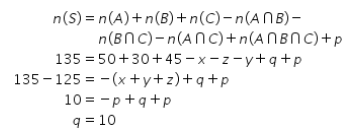
Diperoleh bahwa banyak siswa yang menyukai ketiga olahraga adalah 10.

Selanjutnya, akan ditentukan nilai kebenaran dari setiap pilihan satu per satu.

Pilihan 1: Banyaknya murid yang menyukai basket, renang, dan kasti adalah 10 orang.

Seperti pada perhitungan sebelumnya, diperoleh bahwa banyak siswa yang menyukai ketiga olahraga (basket, renang, dan kasti) adalah 10.

Oleh karena itu, pilihan 1 bernilai BENAR.

Pilihan 2: Banyaknya murid yang hanya menyukai basket dan renang adalah x − 10 orang.

Banyak murid yang hanya menyukai basket dan renang adalah n(A ∩ B) − n(A ∩ B ∩ C) = x − 10..

Oleh karena itu, pilihan 2 bernilai BENAR.

Pilihan 3: Banyaknya murid yang menyukai renang atau kasti adalah 75 orang.

Banyak murid yang menyukai renang adalah 30 dan banyak murid yang menyukai kasti adalah 45, maka banyak murid yang menyukai renang atau kasti adalah 75 orang.

Oleh karena itu, pilihan 3 bernilai BENAR.

Pilihan 4: Banyaknya murid yang menyukai tepat dua jenis olahraga adalah x + y + z orang.

Perhatikan perhitungan berikut!

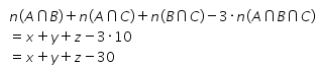
Oleh karena itu, pilihan 4 bernilai SALAH.

Dengan demikian, dapat disimpulkan bahwa pernyataan 1, 2, dan 3 SAJA yang benar.

Jadi, jawaban yang tepat adalah A.

Topik : Aljabar dan Fungsi

Subtopik : Konsep Dasar Fungsi Komposisi dan Invers

Level Kognitif : MOTS

3. Diberikan dua buah fungsi

Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas P dan Q berikut yang benar?

1. Kuantitas P lebih besar daripada Q.
2. Kuantitas P lebih kecil daripada Q.
3. Kuantitas P sama dengan Q.
4. Tidak dapat ditentukan hubungan antara kuantitas P dan Q.

 

Kunci Jawaban : C

Pembahasan :

Langkah Pertama: Tentukan nilai kuantitas P.

Nilai kuantitas P dapat ditentukan dengan cara sebagai berikut.

Langkah Kedua: Tentukan nilai kuantitas Q.

Nilai kuantitas Q dapat ditentukan dengan cara sebagai berikut.

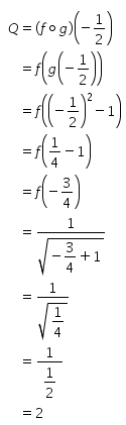
Langkah Ketiga: Tentukan hubungan nilai kuantitas P dan Q.

Karena P = 2 dan Q = 2, maka diperoleh hubungan P = Q.

Dengan demikian, diperoleh kuantitas P sama dengan Q.

Jadi, jawaban yang tepat adalah B.

4. KPK  dari dua buah bilangan prima x dan y adalah 14, dengan x > y. Nilai dari 3x-y adalah…

1. -1
2. 13
3. 19
4. 21
5. 23

 

Kunci Jawaban: C
Pembahasan:

KPK dari 2 bilangan x dan y adalah 14.

Ketika kita jabarkan 14=2×7, maka 2 bilangan tersebut adalah  x=7 dan y=2.

Jadi, 3x – y = 37 – 2 = 21 – 2= 19

Maka, jawaban yang benar adalah C.

Baca juga: Latihan Soal TPS UTBK 2021 Pengetahuan Kuantitatif

5. Diketahui r = 2019, s = 2018, t = 2017

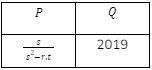
Manakah hubungan yang benar antara kuantitas P dan Q ?

1. P>Q
2. Q>P
3. P=Q
4. Informasi yang diberikan belum cukup menjawab pertanyaan ini

 

Kunci Jawaban: B

Pembahasan:

Diketahui r = 2019, s = 2018, t = 2017

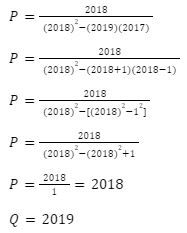
Jadi,  hubungan antara P dan Q adalah Q>P

Maka, jawaban yang benar adalah B.

6. Diketahui dua buah bilangan yaitu  dan . Bilangan yang harus ditambahkan sehingga didapat rata-rata yaitu  adalah…

 

Kunci Jawaban: B

Pembahasan:

Dicari adalah rata – rata dari 3 nilai sehingga perhitungannya menjadi:

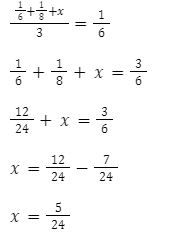
Jadi, bilangan yang harus ditambahkan adalah 

Maka, jawaban yang benar adalah B.

Baca juga: Kumpulan Soal TKA dan TPS UTBK SNBT

7. Manakah pernyataan yang benar jika |2x – 5| <3  dengan x adalah bilangan bulat?

1. HP = {1,2,3,4}
2. HP ={x|1 < x < 4, x∈Ζ}
3. Jumlah seluruh nilai x adalah 10
4. Hasil kali seluruh nilai x adalah 6

 

1. (1), (2) dan (3) SAJA yang benar
2. (1) dan (3) SAJA yang benar
3. (2) dan (4) SAJA yang benar
4. Hanya (4) SAJA yang benar
5. Semua pilihan jawaban benar

 

Kunci Jawaban: C

Pembahasan:

1. Lakukan dengan subtitusi HP ={1,2,3,4}

x=1 masukkan ke persamaan |2x – 5| <3

|2 (1) – 5| <3

3 < 3 maka salah pernyataan 1) jadi x = 1 bukan termasuk HPnya

x = 2 masukkan ke persamaan |2(x) – 5| <3

|2 (2) – 5| <3

1 < 3 maka benar pernyataan 1) jadi x = 2 termasuk HPnya

x = 3 masukkan ke persamaan |2(x) – 5| <3

|2 (3) – 5| <3

1 < 3 maka benar pernyataan 1) jadi x = 3 termasuk HPnya

x = 4 masukkan ke persamaan |2(x) – 5| <3

|2 (4) – 5| <3

3 < 3 maka benar pernyataan 1) jadi x = 4 bukan termasuk HPnya

Jadi pernyataan 1) salah

2. Dapat dilihat dari penjelasan pernyataan 1) bahwa yang termasuk HPnya adalah {2,3} maka HP = {x|1 < x < 4, x∈Ζ }

Jadi pernyataan 2 benar.

3. Pernyataan 3) salah karena 2 + 3 = 5 

4. Pernyataan 4) benar karena 2 × 3 = 6

Jadi jawaban yang tepat yaitu (2) dan (4) saja yang benar

Maka, jawaban yang benar adalah C.

8. Jika dan  adalah akar – akar persamaan 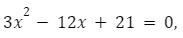 maka nilai dari = …

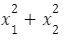1. 8
2. 5
3. 4
4. 3
5. 2

 

Kunci Jawaban: E

Pembahasan:

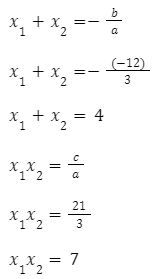
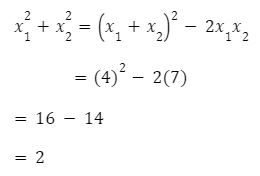
Maka, jawaban yang benar adalah E.

Masih kurang? Wah, kamu wajib daftar Brain Academy sih. Ada modul dan ribuan soal, sesi konsultasi via google meet atau chat, tes minat bakat, kelas pengembangan diri, ribuan latihan soal, dan masih banyak fitur lain yang bantu kamu masuk PTN favorit. Yuk, coba kelas gratis di cabang terdekat dari kotamu! Psst, kamu juga bisa latihan dengan tryout UTBK gratis di ruanguji

Tim Penyusun:

Firdha Dwishafarina