Transformasi Geometri: Pemahaman Konsep & Latihan Soal

Masih bingung dengan materi transformasi geometri? Yuk, pelajari konsep, latihan soal, dan pembahasannya di artikel ini!

—

Hai Brainies nggak kerasa banget UTBK makin dekat. Gimana nih persiapan kamu? 

Kakak-kakak Star Master Teacher udah ngumpulin data persebaran materi UTBK dari beberapa tahun belakangan ini loh. 

Nah, kalo kamu liat tuh, transformasi geometri cukup sering muncul di soal UTBK. Bisa dibilang materi transformasi geometri itu cukup mudah. Jadi, lumayan banget kan kalo kamu bisa jawab soal transformasi geometri dengan cepat dan tepat. Intinya sih, harus perdalam konsep dan latihan soal-soalnya. Yuk langsung aja kita mantepin lagi konsepnya!

Pengertian Transformasi Geometri

Apa itu transformasi geometri? Coba kita bedah kedua kata tersebut terlebih dahulu ya. Transformasi berarti perubahan sebuah struktur menjadi bertambah, berkurang, atau tertata kembali. Sementara itu, geometri adalah sesuatu yang berkaitan dengan bangun, garis, titik, sudut, bidang, dan pengukurannya.

Nah, dari situ kita bisa memahami bahwa, transformasi geometri adalah perubahan posisi dan ukuran suatu benda atau objek pada bidang geometri seperti garis, kurva, atau titik.

Pada kehidupan sehari-hari, transformasi geometri biasanya dimanfaatkan untuk pembuatan karya-karya seni atau desain arsitektur.

Jenis-Jenis Transformasi Geometri

Nah, transformasi geometri itu ada 4 jenis:

• Translasi
• Refleksi
• Rotasi
• Dilatasi

Waktu SMP kamu udah pernah belajar ini, bedanya di SMA transformasi geometri lebih detail dan menggunakan pendekatan matriks.

1. Translasi atau Pergeseran

Disini translasi maksudnya semua titik dan garis dengan jarak dan arah yang telah ditentukan mengalami pergeseran. Nah, untuk caranya nggak jauh beda dengan yang udah pernah diajarin waktu SMP. Tapi, kayak yang udah disinggung dari awal, menggunakan matriks supaya lebih mudah dalam perhitungannya.

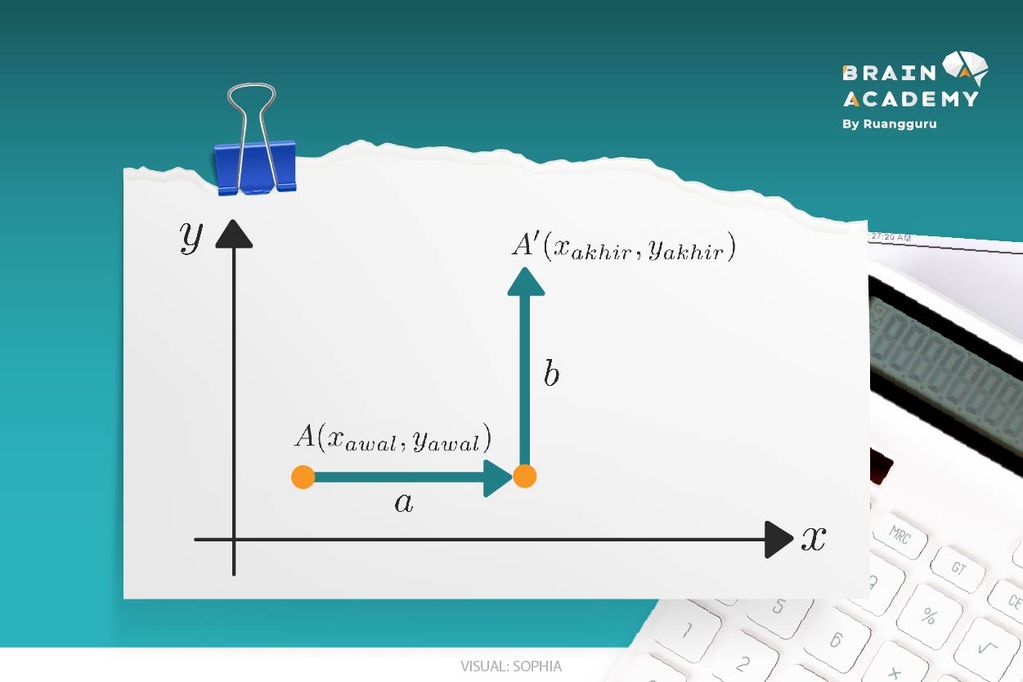
Untuk menghitungnya, jadi kaya gini nih:

Misal ada suatu titik 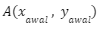ditranslasikan sejauh (a,b), bayangan titik A yaitu

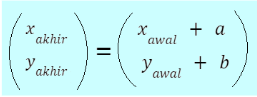
*Note: Koordinat bayangan bisa juga dituliskan dengan (x’ ,y’)

Supaya kamu bisa menerapkan rumusnya, langsung masuk ke contoh soal ya! Eits tapi kita coba yang agak beda dari biasanya nih, yaitu soal translasi garis.

Latihan Soal Translasi

Diketahui garis k dengan persamaan y=8x-2 ditranslasikan oleh

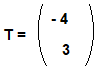
Persamaan bayangan garis k setelah ditranslasi adalah…

1.  y = 2x – 23
2.  y = 4x + 33
3. -y = 8x – 33
4. -y = 4x – 23
5.  y = 8x + 33

2. Refleksi atau Pencerminan

Kayak namanya aja nih yaitu pencerminan, jadi suatu titik akan dicerminkan sesuai dengan jarak yang udah ditentukan. Titik awal dan bayangannya berada dalam satu garis lurus yang tegak lurus  dengan cerminnya. 

Nah, kamu masih inget gak jenis-jenis refleksi? Gak boleh lupa ya, karena konsep di jenjang SMA ini adalah lanjutan dari konsep refleksi waktu kamu SMP dulu. 

Konsep refleksi yang sudah pernah kamu pelajari itu akan dihubungkan sama matriks. Jadi dari situ kita bisa tau matriks refleksi untuk tiap jenis refleksinya.

Ohya, untuk refleksi garis mirip kayak tahap translasi garis yang udah kita bahas. Nah, supaya kamu paham maksud dari tabel di atas, langsung aja kita bahas soalnya.

Latihan Soal Refleksi

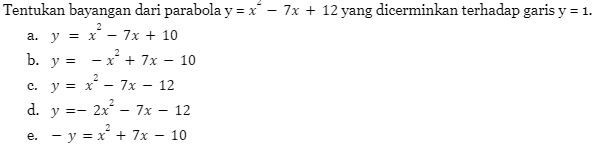
Jadi gitu ya guys, dari soal refleksi ini bisa dibuat berbagai variasi, makanya kamu harus pastikan sudah paham konsep dari semua jenis refleksinya ya.

Baca juga: Latihan Soal dan Pembahasan UTBK

3. Rotasi atau Perputaran

Maksud rotasi pada materi transformasi geometri ini adalah perputaran titik sesuai dengan komponen rotasinya, seperti pusat rotasi (0,0) dan sudut rotasi. Jadi beda ya sama 2 jenis sebelumnya.

Ohya, di SMA ini untuk rotasi kamu bakal belajar titik pusat selain (0,0) dan sudut-sudutnya yang nggak terbatas, jadi lebih luas gitu deh. 

Kamu nggak boleh lupa nih sama syarat rotasi:

Kalo bernilai negatif jika putarannya searah jarum jam.

Tapi akan bernilai positif jika putarannya berlawanan arah jarum jam.

Nggak boleh kebalik ya!

Agak kurang nih kalo cuma tau rumus nya aja tanpa bahas soal. Yuk lah langsung aja kita masuk ke soal rotasi.

Latihan Soal Rotasi

Sebuah titik Z(8, 13) diputar sejauh 60° berlawanan arah jarum jam dengan pusat rotasi P(2,-1). Bayangan dari titik Z adalah…

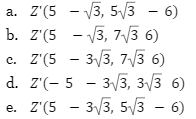
Next, kita masih ada 1 lagi nih jenis transformasi geometri yang harus dibahas, apalagi kalo bukan dilatasi.

4. Dilatasi atau Perubahan Ukuran Objek

Kamu harus tau nih, jadi objek dari ketiga jenis transformasi sebelumnya (translasi, refleksi dan rotasi) nggak akan berubah ukurannya. Tapi untuk suatu objek yang didilatasikan akan mengalami perubahan ukuran. Bisa membesar atau mengecil.

Eits, tapi dilatasi tidak mengubah bentuk, jadi cuma ukurannya aja ya, dan untuk prinsipnya tetap pakai matriks ya.

Ada dua hal yang harus kita perhatikan dalam dilatasi:

1. Pusat dilatasi
   Pusatnya bisa (0,0) atau bisa di titik mana saja.
2. Faktor Skala (k)

Oke, sekarang kita liat nih cara untuk mendapatkan bayangan yang di dilatasikan:

Dilatasi dengan pusat (0,0)

Jika suatu titik 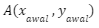didilatasi sebesar k dengan pusat dilatasi (0,0), maka bayangan titik A adalah

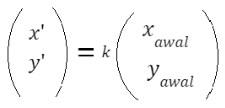
Dilatasi dengan pusat (a,b)

Jika suatu titik 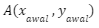didilatasi sebesar k dengan pusat dilatasi (0,0), maka bayangan titik A adalah 

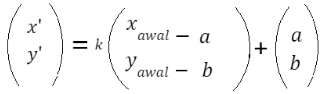
Oke sekarang kita liat yuk contoh soal di bawah ini, supaya kamu tau cara aplikasikan rumus-rumus di atas.

Latihan Soal Dilatasi

Jika kurva 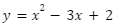didilatasi dengan pusat (0,0) dan faktor skala -1/2 , maka kurva bayangannya adalah…

—

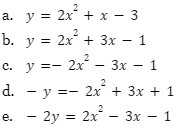
Nah, kita udah bahas 4 soal dari masing-masing jenis transformasi nih. Wah akhirnya selesai juga bahas keempat jenis transformasi geometri nih. Ohya, aku juga mau ingetin ke kamu kalo soal transformasi geometri tuh bisa digabungkan semua jenisnya dalam 1 soal. Makanya, harus sering latihan soal di Brain Academy ya! Soal yang selalu diupgrade dan pastinya ada video pembahasannya, mantep kan. Langganan sekarang aja, dadah!

Referensi:

Wirodikromo, S. dan Darmanto, M. (2019) Matematika untuk SMA/MA Kelas XI kelompok Wajib 2. Jakarta: Erlangga.